在计算机中,整数有两种类型的编码,一种只能表示非负数,即无符号编码,另外一种可以表示负数,即有符号编码。
在C语言中支持有符号数和无符号数,而Java只支持有符号数,下面就来看下它们是如何编码的。
无符号数编码
假设一个整数用二进制表示的话有w位,[Xw-1,Xw-2,….,X0],那么用函数B2U(Binary to Unsigned)表示无符号数,则
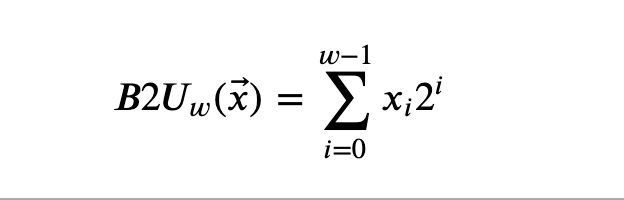
B2U([0001]) = 0 * 2^3 + 0 * 2^2 + 0 * 2^1 + 1 * 2^1 = 0 + 0 + 0 + 0 = 1
B2U([0101]) = 0 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^1 = 0 + 4 + 0 + 0 = 5
下面我们来看下无符号数的范围,对于w为的无符号数,它的最小值就是[000000…000],也就是0,对于最大值就是[1111…111],也就是2^w-1
以w为4为例
B2Umax = 2^4 - 1 = 15
B2Umin = 0
有符号数编码
补码
补码(two’s-complement)是最常见的有符号数编码,在补码中,符号的最高位表示负权,如果用函数B2T(Binary to Two’s-complement)表示,则

最高位Xw-1也称为符号位,它的权重为-2^w-1,所以当符号位被设置为1时,表示值为负,当被设置为0时,值为非负
B2T([0001]) = -0 * 2^3 + 0 * 2^2 + 0 * 2^1 + 1 * 2^1 = 0 + 0 + 0 + 0 = 1
B2T([1001]) = -1 * 2^3 + 0 * 2^2 + 0 * 2^1 + 1 * 2^1 = -8 + 0 + 0 + 1 = -7
下面来看下补码所能表示的范围。对于补码来说,它的最小值为[1000…00],也就是最高位设置为负权,同时清除其他为0,而最大值为[0111..11],清除负权,其他值设置为1.
Tmin = -2^(w-1)
Tmax = 1 * 2^(w-2) + 1 * 2^(w-3) + ... + 1 * 2^0 = 2^(w-1) - 1
以w为4为例
Tmax = - 2^(4-1) = -8
Tmin = 2^(w-1) - 1 = 7
反码
反码(one’s complement),除了最高位的权是-(2^(w-1) - 1),而不是-2^(w-1),其他和补码一样
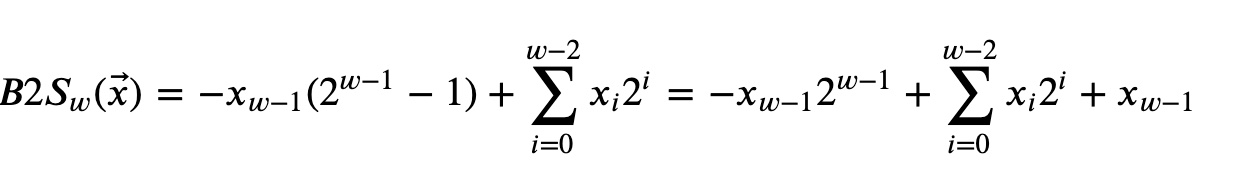
可以看到当Xw-1=0时,反码也补码一致,也就是对于正整数,反码和补码一直,而当Xw-1=1,也就是负数时,反码比补码大1,
原码
原码(sign-magnitude),最高位是符号位,用来决定剩下的位应该是负权还是正权
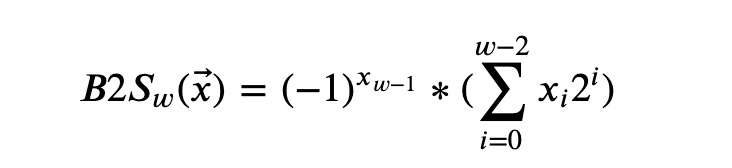
在原码和反码中,0都有两种表示方式。它们都把[000…000]解释为+0,而-0在原码中表示[1000…000],而在反码中表示[1111…11]
无符号数与有符号数转换
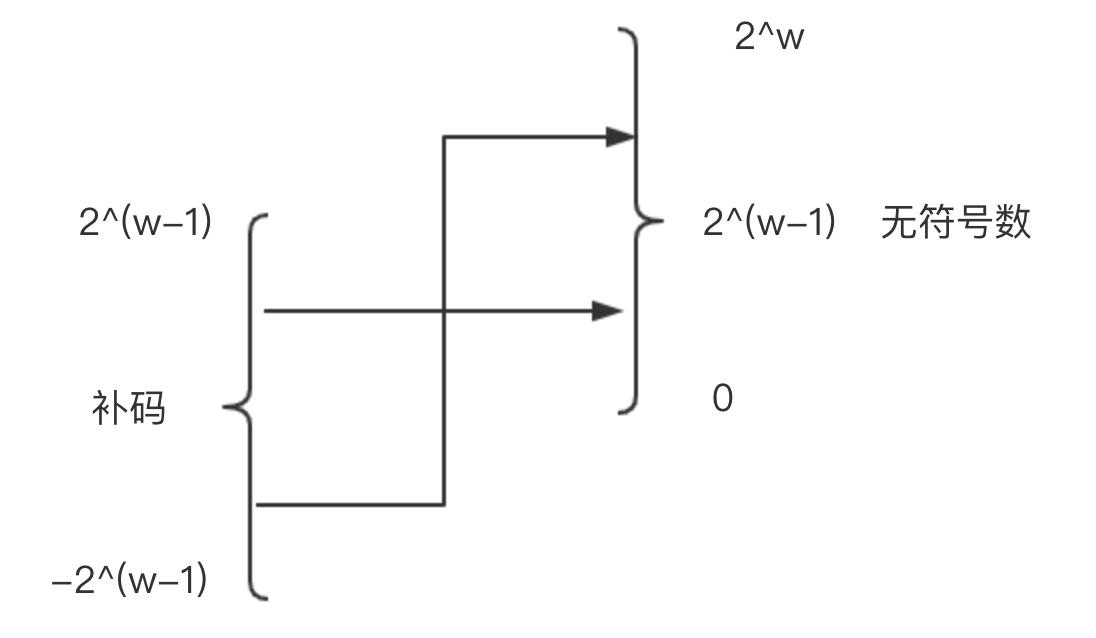
补码转为无符号数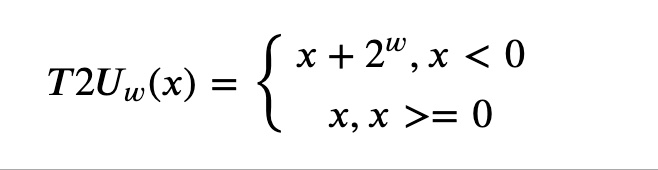
无符号数转为补码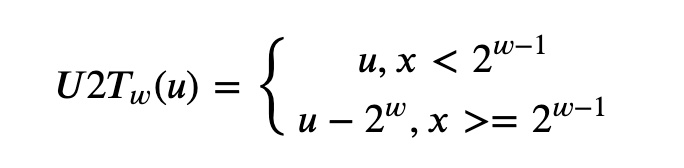
例如
T2U16(-12345) = -12345 + 2 ^ 16 = 53191
U2T16(53191) = 53191 - 2 ^ 16 = -12345
也就是16进制0xCFC7既是-12345的补码表示,也是53191的无符号数表示



